[ML] Ensemble (앙상블) - [3] Approach 2. Boosting - Adaboost, Gradient Boost

Posted Jan 3, 2025 Updated Jan 3, 2025

By minsuk Kang

views 9 min read

Ensemble Series

[1] Ensemble, Combination Strategy: Voting, Averaging, Stacking
[2] Approach 1. Bagging - Random Forest
[3] Approach 2. Boosting - AdaBoost, Gradient Boost

지난 2편에서는 개별 학습기 간 의존성이 약하며, 동시에 생성하는 병렬화 방식인 배깅 ^Bagging 방식을 다루었다.

이번 3편에서는 개별 학습기 간 의존성이 강하며, 순차적으로 생성하는 연속화 방식인 부스팅 ^Boosting 방식과, 대표적인 AdaBoost와 Gradient Boost, 두 방법론을 설명한다.

Boosting

부스팅 ^Boosting 은 여러 개의 약한 학습기 ^{Weak Learner} 를 연결하여 강한 학습기 ^{Strong Learner} 를 만드는 방법이다.

부스팅의 작동 매커니즘은 다음과 같다.

초기 훈련 세트로부터 기초 학습기 ^{Base Learner} 를 훈련
기초 학습기에서의 오차를 보정하도록 다음 기초 학습기를 훈련
1 ~ 2번 과정을 T번 반복 후, T개의 기초 학습기에 대해 가중 결합하여 최종 예측

이와 같이, 부스팅은 앞의 모델을 순차적으로 보완해 나가는 방식이다.

AdaBoost

AdaBoost (Adaptive Boosting)는 가법 모델 ^{Additive Model} 의 대표적인 예로, 이전 모델이 과소적합했던 훈련 샘플의 가중치를 더 높여 모델을 순차적으로 보완한다. ¹

AdaBoost

첫 학습기가 예측이 잘못된 훈련 샘플의 가중치를 상대적으로 높이고, 두 번째 학습기는 업데이트된 가중치를 통해 다시 훈련하고 예측을 수행한다. 이 과정이 계속 반복된다.

Algorithm

AdaBoost는 지수 손실 함수 ^{Exponential Loss Function} 를 최소화하도록 설계되었다.

각 샘플의 가중치 초기화
\[w_i^{(1)} = \frac{1}{m}, \quad i = 1, 2, \dots, m\]
- $m$: 샘플 수
반복 수행 $( j = 1, 2, \dots, n )$
1. 학습기 훈련: 주어진 데이터와 가중치로 학습기 훈련
2. 오류율 계산: 가중치를 사용해 오류율 계산
  \[e_j = \frac{\sum_{i=1}^m w_i^{(j)} \cdot \mathbb{1}(y_i \neq h_j(x_i))}{\sum_{i=1}^m w_i^{(j)}}\]
  - $h_j(x_i)$: $i$번째 샘플에 대한 $j$번째 학습기의 예측값
  - $\mathbb{1}(\cdot)$: 조건에 따라 1 ^True 또는 0 ^False 을 반환하는 지시 함수
3. 가중치 계산: 학습기의 성능에 따라 가중치 설정
  \[\alpha_j = \eta \ln\left(\frac{1 - e_j}{e_j}\right)\]
  - $\eta$: 학습률 하이퍼파라미터 (1을 기준으로 학습기가 정확할수록 증가, 랜덤 예측일수록 0에 근접)
4. 샘플 가중치 업데이트: 잘못 예측된 샘플에 더 많은 가중치 부여
  \[w_i^{(j+1)} = w_i^{(j)} \cdot \exp\left(-\alpha_j \cdot y_i \cdot h_j(x_i)\right)\]
5. 정규화: 모든 가중치의 합이 1이 되도록 정규화
최종 모델 결합: 모든 학습기의 결과를 가중합하여 예측
\[H(x) = \text{sign}\left(\sum_{j=1}^n \alpha_j \cdot h_j(x)\right)\]

Code

AdaBoost는 Scikit-learn의 AdaBoostClassifier, AdaBoostRegressor 클래스를 활용해 구현할 수 있다.

  
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier

ada_clf = AdaBoostClassifier(
  DecisionTreeClassifier(max_depth=1), n_estimators=30,
  learning_rate=0.5, random_state=42
)
ada_clf.fit(X_train, y_train)

위 코드는 200개의 DecisionTree를 기반으로 AdaBoost 분류기를 학습한다.

Gradient Boost

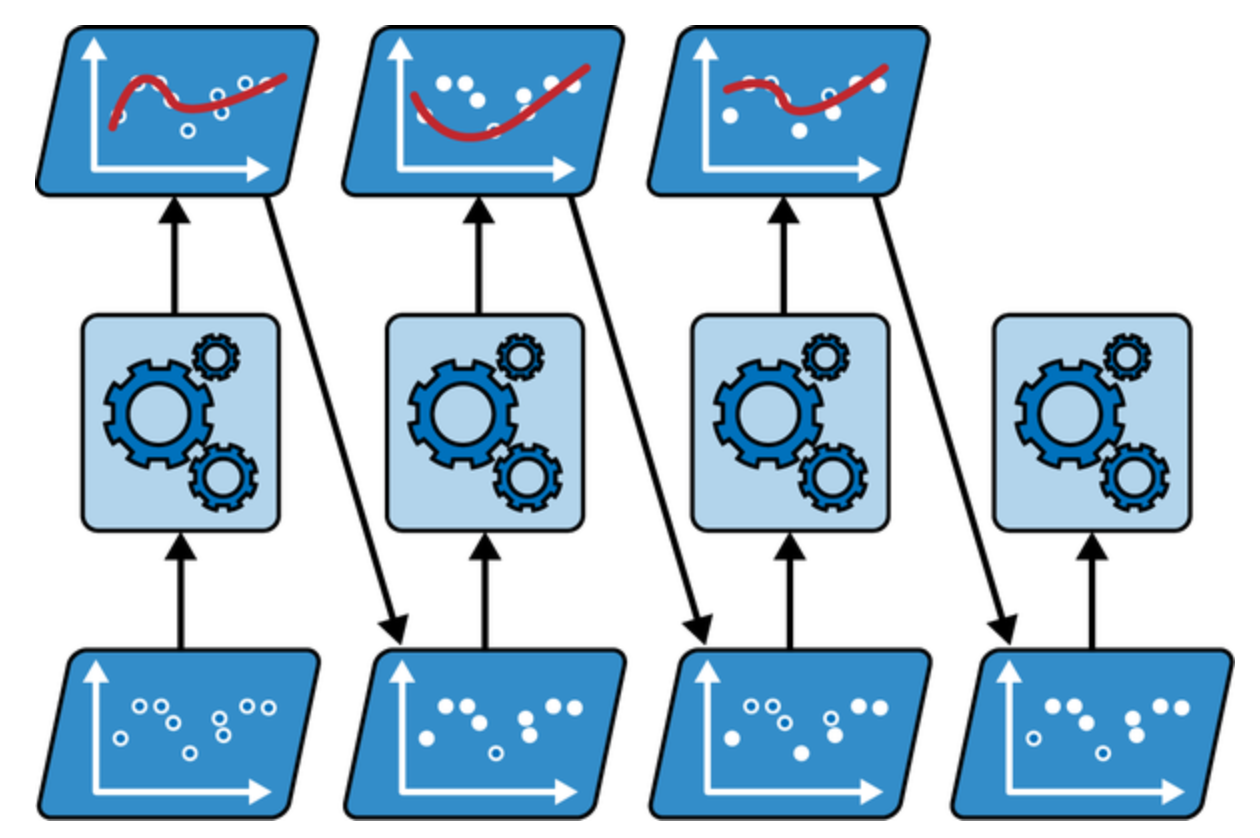
Gradient Boost는 각 단계에서 잔차 ^Residual 를 계산하고 이를 예측하도록 학습기를 훈련한다.

매 반복마다 샘플의 가중치를 수정하는 AdaBoost와는 달리, 이전 예측기의 잔차에 새 예측기를 학습하는 방식이다.

이는 손실 함수를 최소화하기 위해 예측기의 모델 파라미터를 조정하는 경사 하강법과 비슷하다.

Algorithm

정의한 손실 함수를 최소화하는 방식으로 모델을 반복적으로 학습한다.

손실 함수 선택
- 일반적으로 회귀 문제일 경우 MSE, 분류 문제일 경우, Log Loss를 선택한다.
1. MSE
  - 손실 함수: $L(y, F(x)) = \frac{1}{2} (y - F(x))^2$
  - 잔차: $r_i^{(j)} = y_i - F_{j-1}(x_i)$
2. Log Loss
  - 손실 함수: $L(y, F(x)) = -\sum_{i=1}^m \left[ y_i \log(F(x)) + (1 - y_i) \log(1 - F(x)) \right]$
  - 잔차: $r_i^{(j)} = y_i - \sigma(F_{j-1}(x_i))$
    - $\sigma$: 시그모이드 함수
초기 모델 초기화
- 초기 모델 $F_0(x)$는 손실 함수의 최적화 값을 사용한다.
  \[F_0(x) = \arg \min_{\gamma} \sum_{i=1}^m L(y_i, \gamma)\]
반복 수행 $( j = 1, 2, \dots, n )$
1. 잔차 계산: 각 샘플에 대해 현재 손실 함수의 잔차 계산
  \[r_i^{(j)} = -\frac{\partial L(y_i, F_{j-1}(x_i))}{\partial F_{j-1}(x_i)}\]
  - $r_i^{(j)}$: $i$번째 샘플의 잔차
  - $F_{j-1}(x_i)$: 이전 모델의 예측값
2. 잔차 예측 모델 훈련: 새 학습기 $h_j(x)$가 잔차 $r_i^{(j)}$를 예측하도록 훈련
3. 학습률 최적화: 새 학습기가 손실 함수를 최소화하도록 학습률 최적화
  \[\gamma_j = \arg \min_{\gamma} \sum_{i=1}^m L(y_i, F_{j-1}(x_i) + \gamma \cdot h_j(x_i))\]
4. 모델 업데이트: 새 모델은 이전 모델에 학습기 결과 추가
  \[F_j(x) = F_{j-1}(x) + \gamma_j \cdot h_j(x)\]
최종 모델 결합: 모든 학습기의 결과 결합
\[F(x) = \sum_{j=1}^n \gamma_j \cdot h_j(x)\]

Gradient Boost

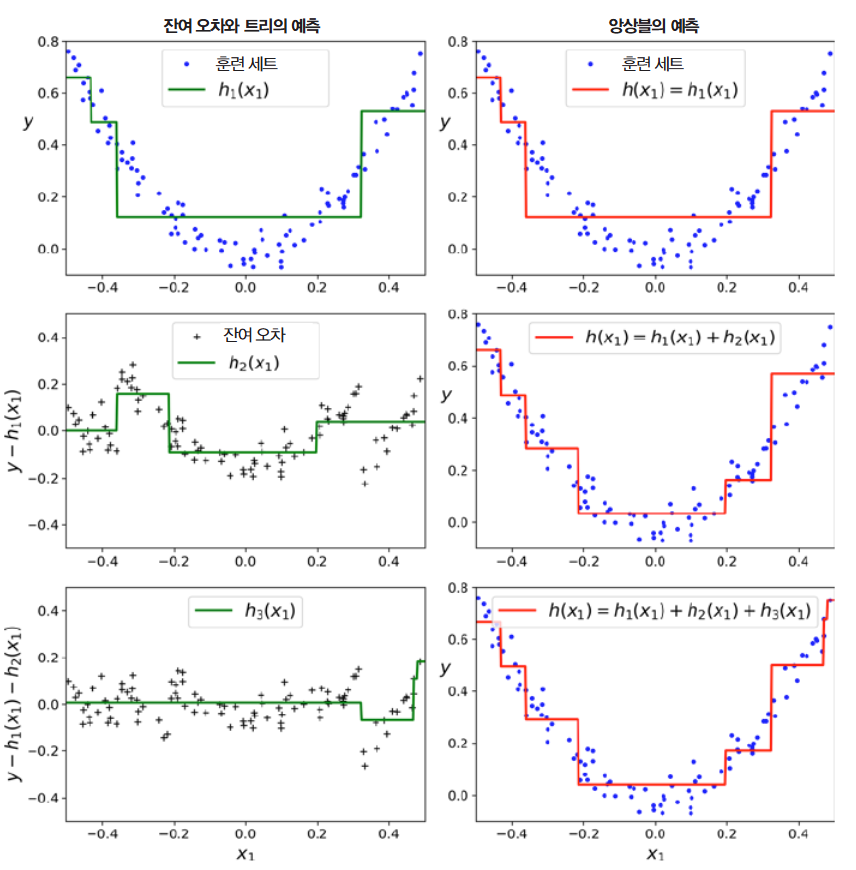
좌측의 각 트리의 예측과 우측의 누적된 트리, 즉 앙상블의 예측을 통해 트리가 앙상블에 추가될 수록 앙상블의 예측이 좋아지는 것을 볼 수 있다.

Code

Scikit-learn의 GradientBoostingClassifier, GradientBoostingRegressor 클래스를 활용해 구현할 수 있다.

  
from sklearn.ensemble import GradientBoostingRegressor

gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=300, learning_rate=0.1, n_iter_no_change=10, random_state=42)
gbrt.fit(X, y)

learning_rate: 각 트리의 기여도
- 낮을 수록 더 많은 트리가 필요하며, 일반적으로 성능이 향상됨
n_estimator: 트리 개수
n_iter_no_change: 성능 검사 트리 개수
- 설정한 개수만큼 트리가 추가되었는데 성능 향상이 없을 경우, 조기 종료하여 최적의 트리 개수 도출
- 낮게 설정하면 과소적합, 높게 설정하면 과대적합

결론

Boosting 기법은 학습기의 순차적 학습을 통해 강력한 예측 성능을 제공하지만, 배깅에 비해 학습 시간이 오래 걸리고 과적합의 위험이 존재한다.

대표적으로, AdaBoost 방법론과 Gradient Boost 방법론이 사용되며, 아래와 같이 정리할 수 있다.

특성	AdaBoost	Gradient Boost
손실 함수	고정된 지수 손실 함수	사용자가 정의 가능 (MSE, Log Loss 등)
업데이트 방식	잘못 분류된 샘플에 가중치를 증가시킴	잔차(Gradient)를 기반으로 새로운 학습기 추가
적용 가능성	주로 분류에 활용	회귀, 분류 모두에 적합
복잡성	단순하고 계산이 빠름	유연하지만 상대적으로 계산 복잡도 증가

최근에는 Gradient Boost의 높은 복잡성을 보완한 XGBoost, CatBoost, LightGBM 등의 부스팅 기반 앙상블 알고리즘이 많이 활용되고 있다.

References

단단한 머신러닝

핸즈온 머신러닝

A decision-theoretic generalization of on-line learning and an application to boosting ↩︎

ML, Ensemble

This post is licensed under CC BY 4.0 by the author.

Ensemble Series

Boosting

AdaBoost

Algorithm

Code

Gradient Boost

Algorithm

Code

결론

References

Trending Tags