[ML] Logistic Regression - [1] 수학적 증명과 이론
Math for ML Series
- [1] Linear Regression - 수학적 증명과 이론
- [2] Logistic Regression - 수학적 증명과 이론
- [3] Softmax Regression - 수학적 증명과 이론
- [4] Support Vector Machine - 수학적 증명과 이론
Logistic Regression Series
- [1] Logistic Regression - 수학적 증명과 이론
- [2] Logistic Regression - 여러 구현 방법 및 해석
Classification
로지스틱 회귀 Logistic Regression 와 소프트맥스 회귀 Softmax Regression 는 분류 문제를 해결하는 기본적인 방법으로, 각각 이진 분류와 다중 클래스 분류에서 활용된다.
본 포스팅은 먼저 Logistic Regression의 수학적 기초를 탐구하며 훈련 및 최적화 과정을 설명한다.
Logistic Regression
로지스틱 회귀는 입력 $x$를 이진 출력 $y \in {0, 1}$로 매핑하는 확률 모델이다.
훈련 함수
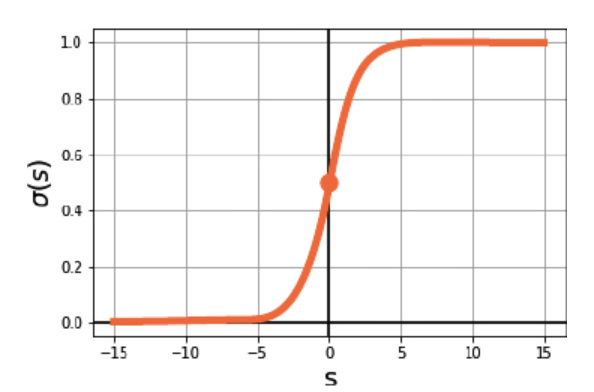
로지스틱 회귀의 출력은 시그모이드 함수 Sigmoid Function 를 활용하여 정의된다.
하나의 데이터 포인트 $x \in \mathbb{R}^{p}$에 대해 예측 확률은 다음과 같다.
\[h_\theta(x) = \sigma(z) = \frac{1}{1 + e^{-z}}, \quad z = x^T\theta\]- $z$: 입력 데이터 $x$와 파라미터 $\theta$ 간의 내적
- $x$: 입력 벡터 ($p \times 1$)
- $\theta$: 파라미터 벡터 ($p \times 1$)
시그모이드 함수의 출력은 $[0,1]$ 범위의 값으로, 클래스 1에 속할 확률로 해석된다.
\[P(y=1|x; \theta) = h_\theta(x), \quad P(y=0|x; \theta) = 1 - h_\theta(x)\]이를 $n$개의 데이터 포인트에 대해 확장한 로지스틱 회귀 모델은 행렬 연산으로 일반화된다.
\[Z = X\theta, \quad H_\theta = \sigma(Z) = \frac{1}{1 + e^{-Z}}\]- $X$: 입력 데이터 행렬 ($n \times p$)
- $\theta$: 파라미터 벡터 ($p \times 1$)
- $Z$: $X$와 $\theta$ 간의 행렬 곱 ($n \times 1$)
- $H_\theta$: 예측 확률 벡터 ($n \times 1$)
손실 함수
로지스틱 회귀는 잘못 분류된 훈련 데이터 포인트에 불이익을 준다.
즉, 잘못된 예측일 수록 큰 페널티를 주어 모델이 학습 과정에서 이를 바로잡을 수 있다.
예측값 $y_{\text{predict}} = h_\theta(x)$가 실제값 $y_{\text{true}}$와 다를수록 큰 페널티를 부과한다.
이 과정에서, 확률 기반의 손실 함수를 정의해야 한다.
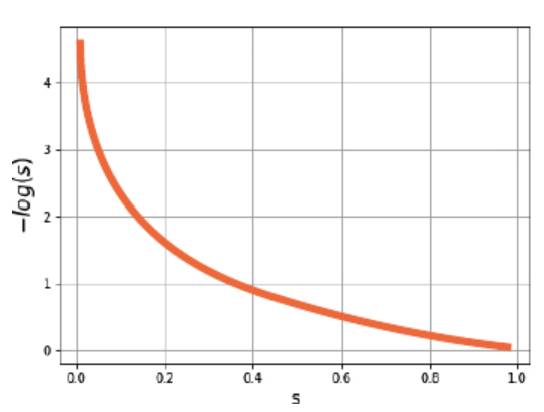
예를 들어, $y_{\text{true}} = 1$인 경우:
\[L = -\log(y_{\text{predict}}), \quad y_{\text{true}} = 1\]- $y_{\text{predict}}$가 $1$에 가까우면 페널티가 작다.
- $y_{\text{predict}}$가 $0$에 가까우면 페널티가 매우 커진다.
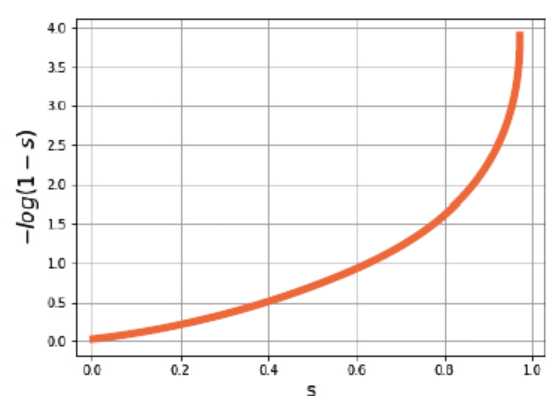
반대로, $y_{\text{true}} = 0$인 경우:
\[L = -\log(1 - y_{\text{predict}}), \quad y_{\text{true}} = 0\]- $1 - y_{\text{predict}}$가 $1$에 가까우면 페널티가 작다.
- $1 - y_{\text{predict}}$가 $0$에 가까우면 페널티가 매우 커진다.
실제값 $y_{\text{true}}$와 예측값 $y_{\text{predict}}$의 조합에 따라, 잘못 분류된 한 개의 훈련 데이터에 대해 다음과 같은 손실 함수가 도출된다.
\[L(y_{\text{true}}, y_{\text{predict}}) = \begin{cases} -\log(y_{\text{predict}}), & \text{if } y_{\text{true}} = 1 \\ -\log(1 - y_{\text{predict}}), & \text{if } y_{\text{true}} = 0 \end{cases}\]$n$개의 전체 데이터에 대해 손실을 평균화하면 다음과 같은 로그 손실 함수 Log Loss 가 정의되며,
이를 크로스 엔트로피 손실 함수 cross-entropy loss function 라고 한다.
\[L(\theta) = -\frac{1}{n} \sum_{i=1}^n \left[ y_i \log(h_\theta(x_i)) + (1 - y_i) \log(1 - h_\theta(x_i)) \right]\]- $y_i$: 실제 레이블
- $h_\theta(x_i)$: 예측 확률
이를 벡터 연산으로 표현하면:
\[L(\theta) = - \frac{1}{n} \left[ y^T \log(H_\theta) + (1 - y)^T \log(1 - H_\theta) \right]\]- $y$: 실제 레이블 벡터
- $H_\theta$: 예측 확률 벡터
최적화
최적화 단계에서는 손실 함수 $L(\theta)$를 최소화하기 위해 미분을 사용하여 최적의 $\theta$를 찾는다.
그러나, 선형 회귀와 달리, 로지스틱 회귀에서는 손실 함수를 최소화하기 위한 닫힌 해 Closed-form Solution 가 존재하지 않는다. 그 이유는 시그모이드 함수가 비선형적이므로, 손실 함수 $L(\theta)$가 $\theta$에 대해 비선형이다.
즉, 미분값 $\frac{\partial L(\theta)}{\partial \theta} = 0$의 해를 대수적으로 계산할 수 없으므로, 수치적 최적화 기법을 사용해야 한다.
다행히도 로지스틱 회귀의 손실 함수는 볼록 함수 Convex Function 이다.
볼록 함수의 성질: 하나의 전역 최솟값만 존재하며 지역 최솟값 local minimum 에 빠질 염려가 없다.
이 성질을 이용하여 확률적 경사 하강법 SGD 또는 미니배치 경사 하강법 Mini-batch Gradient Descent 을 통해 최솟값을 찾을 수 있다.
1. 손실 함수의 도함수
$L(\theta)$를 $\theta$에 대해 미분하면, 손실 함수의 기울기가 다음과 같이 계산된다.
\[\frac{\partial L(\theta)}{\partial \theta} = \frac{1}{n} X^T \left( H_\theta - y \right)\]- $H_\theta$: 예측 확률 벡터 ($n \times 1$)
- $y$: 실제 레이블 벡터 ($n \times 1$)
2. 경사 하강법 Gradient Descent
경사 하강법은 기울기를 따라 손실 함수의 값을 점진적으로 줄이며 $\theta$를 업데이트한다.
\[\theta := \theta - \eta \frac{\partial L(\theta)}{\partial \theta}\]- $\eta$: 학습률(Learning Rate), 기울기를 따라 이동하는 크기를 조절
- 위 식을 반복(iterative)하여 최적의 $\theta$를 찾는다.
3. 확률적 경사 하강법 SGD
전체 데이터셋을 사용하지 않고, 하나의 데이터 포인트에 대해 다음과 같이 업데이트를 진행한다.
\[\theta := \theta - \eta \frac{\partial L(\theta, x_i, y_i)}{\partial \theta}\]- $\frac{\partial L(\theta, x_i, y_i)}{\partial \theta}$는 한 데이터 포인트 $(x_i, y_i)$에 대한 손실의 기울기이다.
- 경사 하강법보다 계산이 빠르고, 큰 데이터셋에서 효과적이다.
4. 미니배치 경사 하강법 Mini-batch Gradient Descent
전체 데이터셋을 $B$개의 미니배치로 나누고, 각 배치에 대해 다음과 같이 $\theta$를 업데이트한다.
\[\theta := \theta - \eta \frac{1}{B} \sum_{i \in \text{batch}} \frac{\partial L(\theta, x_i, y_i)}{\partial \theta}\]- $B$: 미니배치 크기(Batch Size)
- 계산 효율성과 수렴 속도 사이에서 균형을 잡는다.
결론
로지스틱 회귀는 예측 확률을 계산하는 훈련 함수, 페널티를 부여하는 손실 함수, 그리고 최적화를 통해 학습을 진행한다.
손실 함수의 볼록성을 활용해 안정적으로 전역 최솟값을 찾을 수 있다.
| 단계 | 설명 | 수식 |
|---|---|---|
| 훈련 함수 | 시그모이드 함수 $\sigma(z)$를 통해 예측 확률을 계산. | $h_\theta(x) = \frac{1}{1 + e^{-z}}, \quad z = X\theta$ |
| 손실 함수 | 크로스 엔트로피 함수를 사용해 예측값과 실제값 간의 차이에 페널티를 부여. | $L(\theta) = -\frac{1}{n} \sum_{i=1}^n \left[ y_i \log(h_\theta(x_i)) + (1 - y_i) \log(1 - h_\theta(x_i)) \right]$ |
| 최적화 | 손실 함수를 최소화하기 위해 경사 하강법을 사용하여 파라미터 $\theta$를 점진적으로 업데이트. | $\theta := \theta - \eta \frac{\partial L(\theta)}{\partial \theta}, \quad \frac{\partial L(\theta)}{\partial \theta} = \frac{1}{n} X^T \left(H_\theta - y\right)$ |