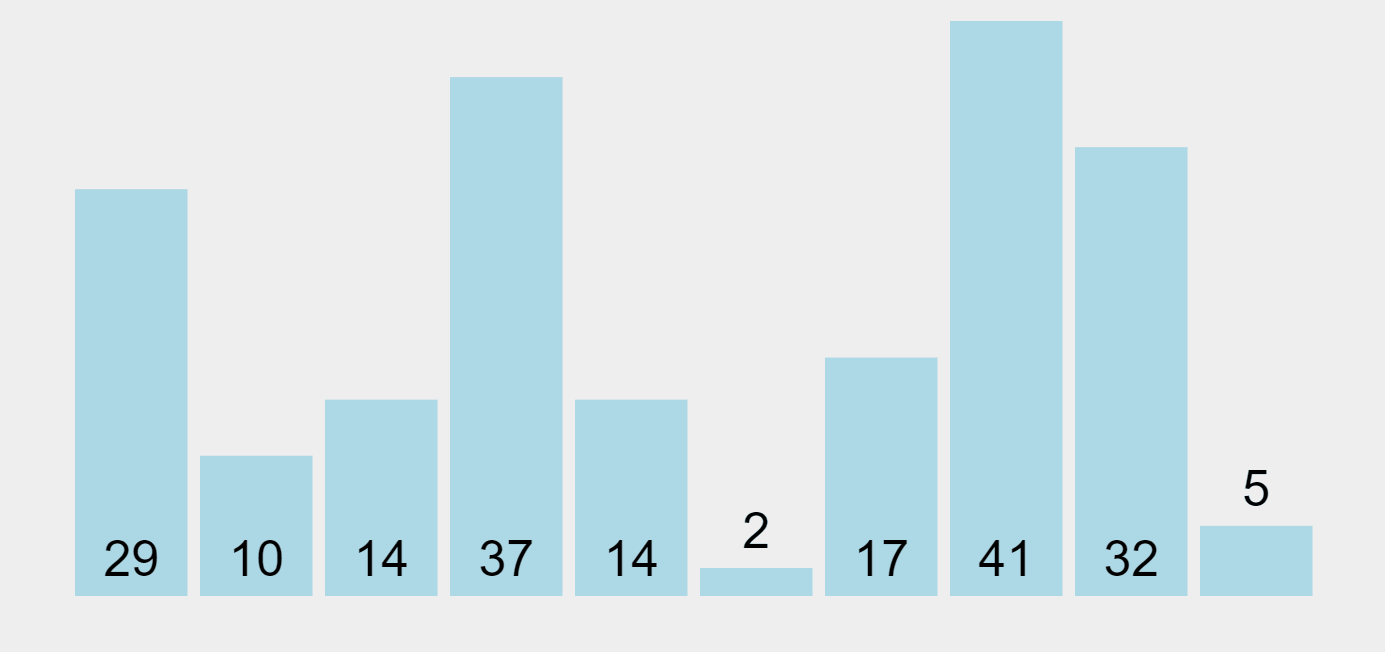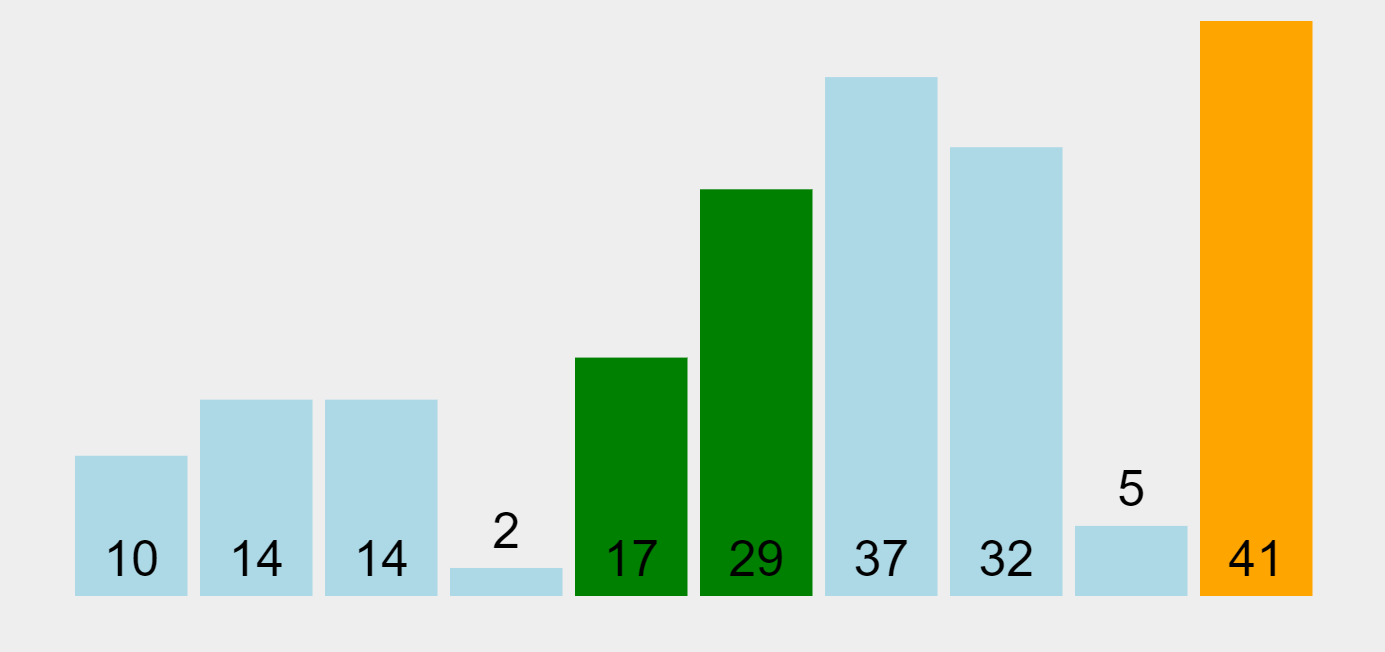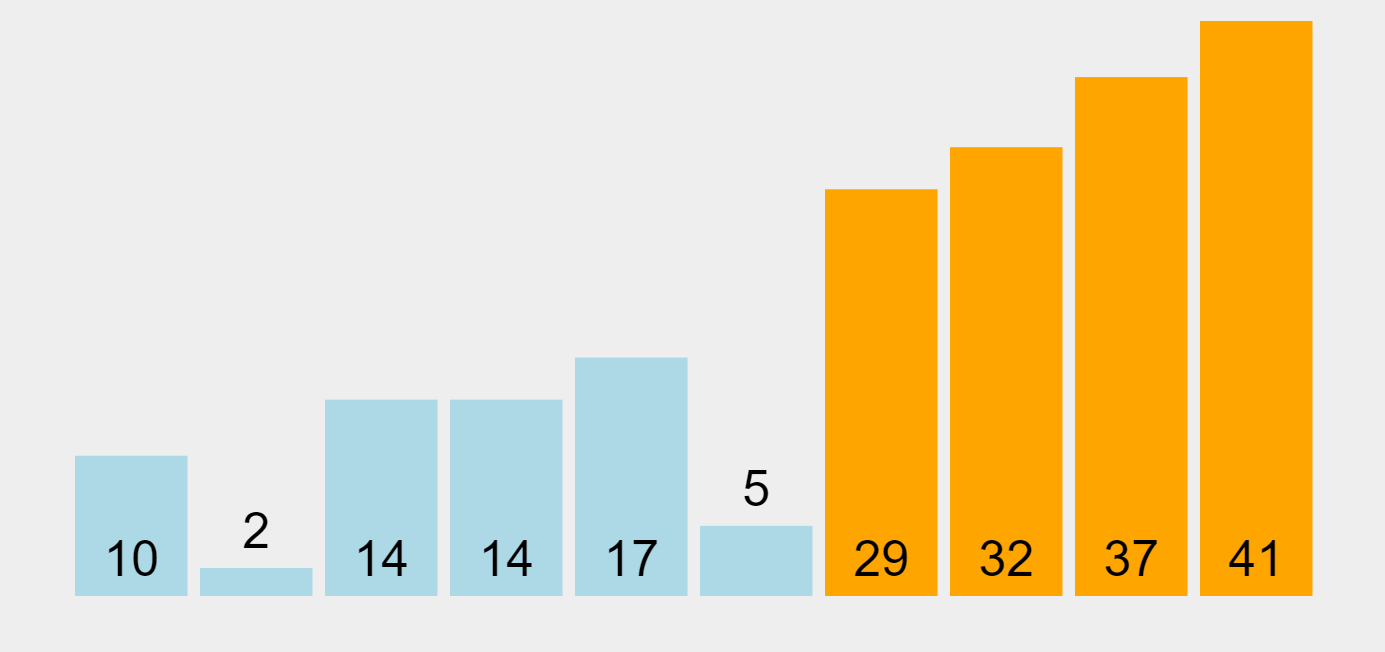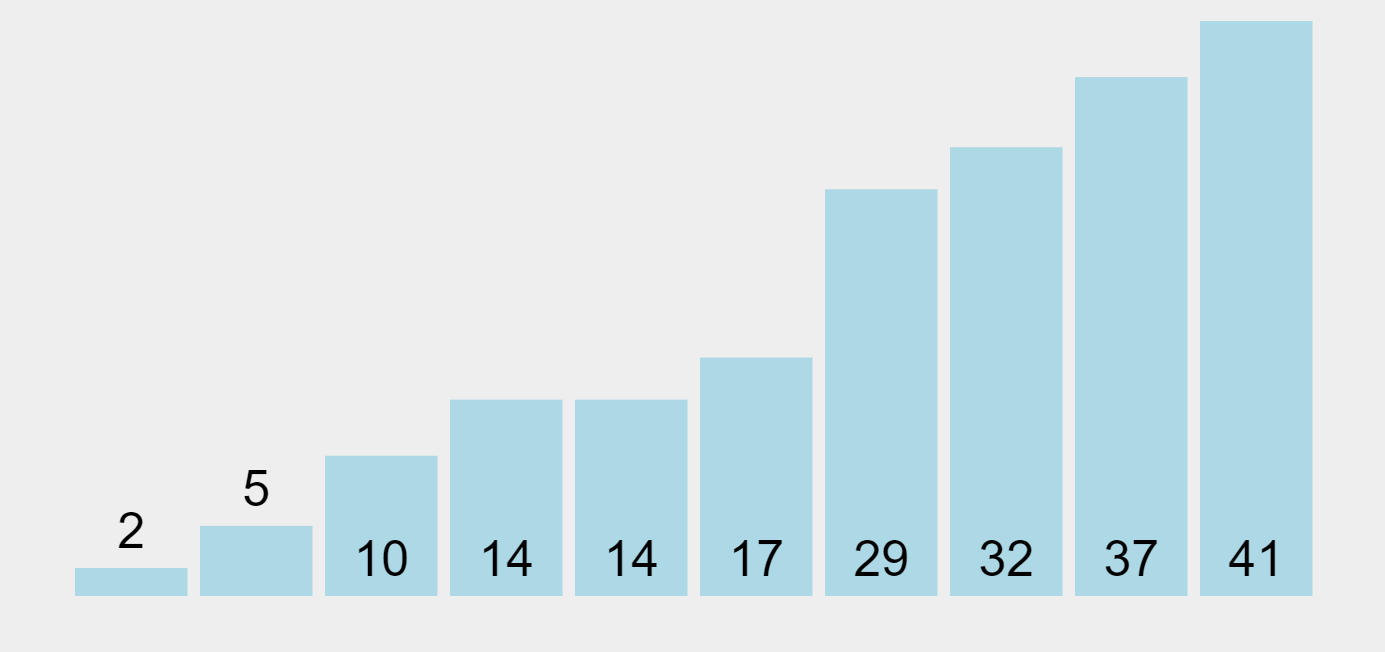[Algorithm] Sort (정렬) - [1] 3가지의 기본 정렬: Selection, Bubble, Insertion Sort
Sort Series
- [1] 3가지의 기본 정렬: Selection, Bubble, Insertion Sort
- [2] 4가지의 고급 정렬: Quick, Merge, Heap, Tim Sort
정렬 알고리즘은 컴퓨터 과학에서 매우 중요한 역할을 수행하며, 알고리즘의 꽃으로 불린다.
이번 글에서는 정렬 알고리즘의 기본적인 개념과 3가지의 기본 정렬 알고리즘, 선택, 버블, 삽입 정렬에 대해 알아보자.
Sort
정렬 알고리즘은 주어진 데이터 집합을 특정 순서로 재배열하는 작업을 수행하며, 정렬의 목표는 가능한 한 비교 횟수와 교환 횟수를 최소화하는 것이다. 효율적인 정렬은 문제 해결의 성능을 크게 좌우한다.
정렬 알고리즘을 평가할 때 중요한 2가지 성질이 있다.
Stable과 Inplace
1) Stable | 같은 값을 가진 데이터의 순서가 정렬 후에도 유지 |
2) In-place | 별도의 추가 메모리 공간을 사용하지 않고 주어진 데이터 공간 내에서 정렬 수행 |
Stable과 In-place를 만족하는 정렬은 바람직한 정렬 알고리즘이라고 할 수 있다.
1. Selection Sort (선택 정렬)
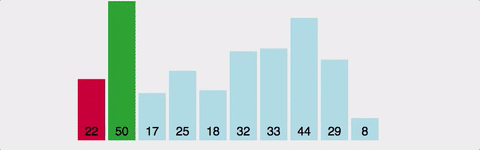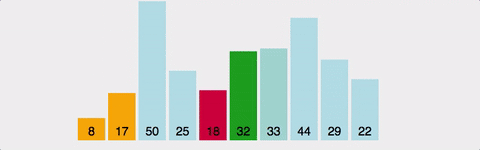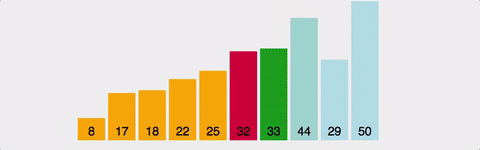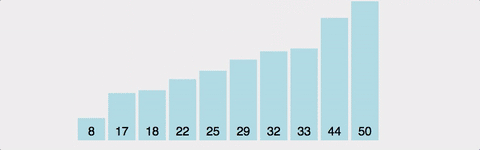
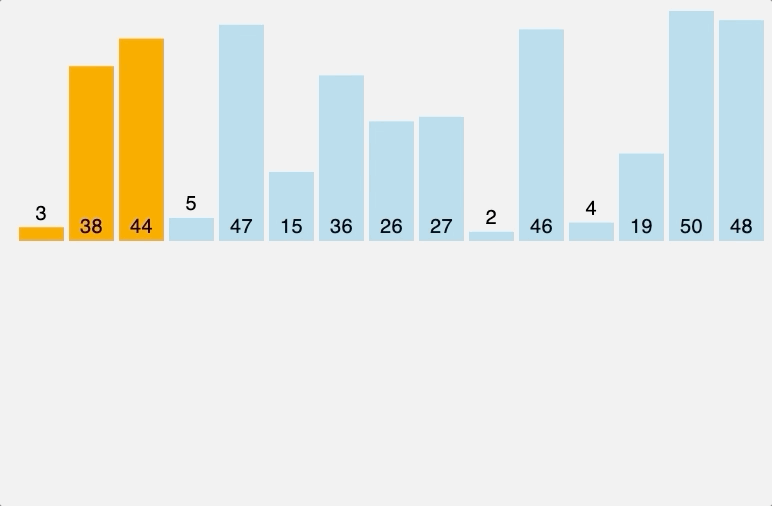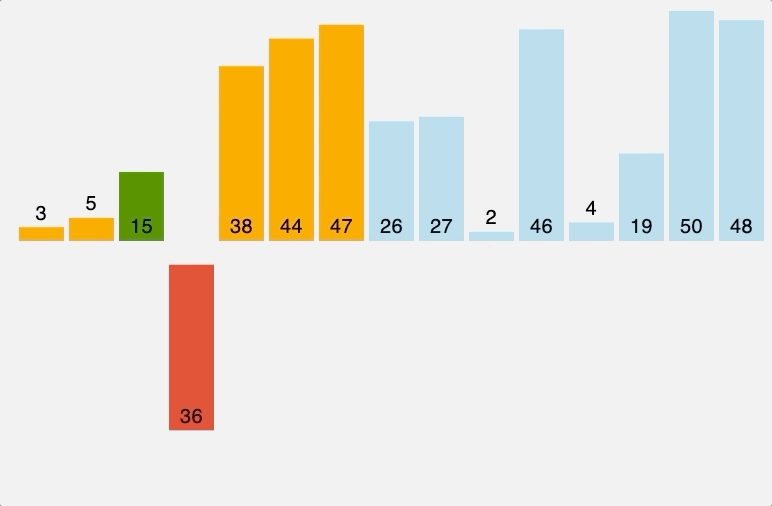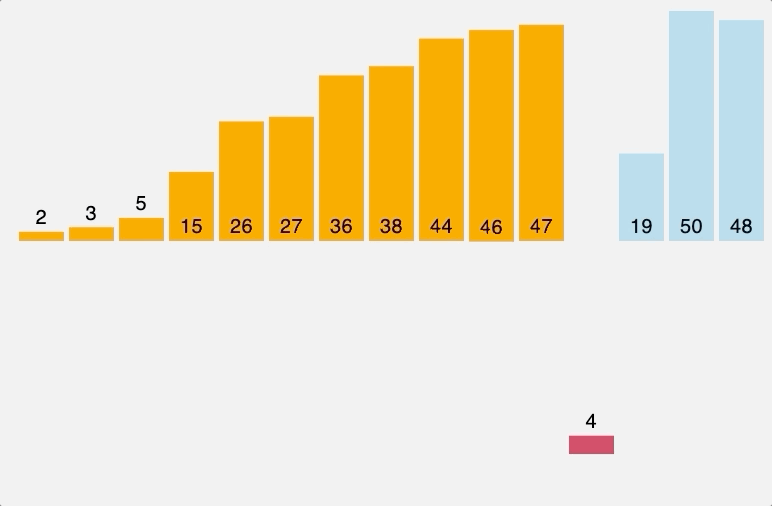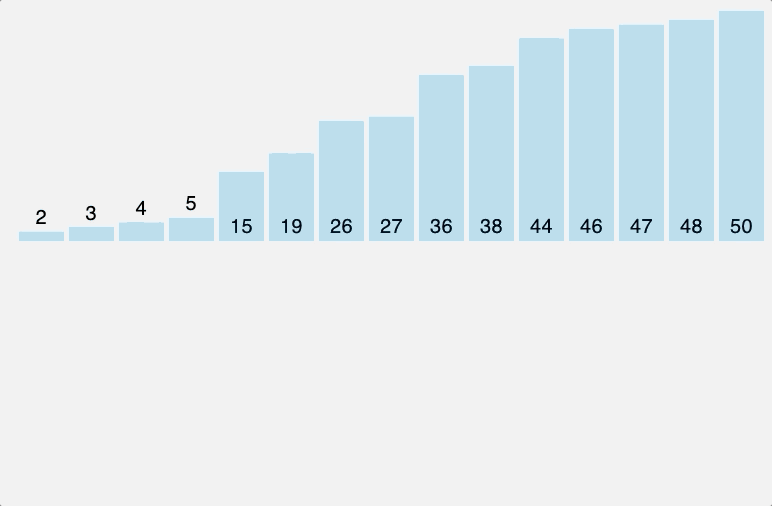
선택 정렬은 최소값 또는 최대값을 찾은 후, 첫 번째 데이터와 교환하고, 이를 제외한 최소값 또는 최대값을 찾아 두 번째 데이터와 교환하는 과정을 반복하는 방식이다. 한 번 선택된 데이터는 그 위치에 고정된다.
Selection Sort
선택 정렬은 최선, 평균, 최악의 경우의 시간 복잡도가 모두 \(O(n^2)\)로 동일하며, 리스트를 2번 선회해야 하므로 매우 비효율적인 알고리즘이다.
1
2
3
4
5
6
7
8
9
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr
2. Bubble Sort (버블 정렬)
버블 정렬은 인접한 두 데이터를 비교해 크기 순서대로 정렬하는 방식으로, 리스트를 순차적으로 순회하면서 큰 값은 오른쪽으로, 작은 값은 왼쪽으로 보내는 과정이 반복된다.
Bubble Sort
버블 정렬은 이미 정렬이 완료된 경우, 시간 복잡도가 \(O(n)\)이지만, 평균, 최악의 경우의 시간 복잡도는 모두 \(O(n^2)\)로 비효율적인 알고리즘이다.
1
2
3
4
5
6
7
8
9
10
11
def bubble_sort(arr):
n = len(arr)
for i in range(n):
swapped = False
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
if not swapped:
break
return arr
3. Insertion Sort (삽입 정렬)
삽입 정렬은 이미 정렬된 부분 리스트에 새로운 데이터를 알맞은 위치에 삽입하면서 정렬을 유지하는 방식이다. 리스트의 두 번째 원소부터 순차적으로 선회하면서 삽입하는 과정이 반복된다.
Insertion Sort
삽입 정렬은 버블 정렬과 동일하게 이미 정렬된 경우, 시간 복잡도가 $O(n)$까지 감소되지만, 보통, 최악의 경우 시간 복잡도는 $O(n^2)$로 비효율적인 알고리즘이다.
1
2
3
4
5
6
7
8
9
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
정리
3가지의 기본 정렬 알고리즘을 정리하면 다음과 같다.
| 구분 | Selection Sort | Bubble Sort | Insertion Sort |
|---|---|---|---|
| Worst Case | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ |
| Avg Case | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ |
| Best Case | $O(n^2)$ | $O(n)$ | $O(n)$ |
| Stable | X | O | O |
| In-place | O | O | O |