[Algorithm] Sort (정렬) - [2] 4가지의 고급 정렬: Quick, Merge, Heap, Tim Sort

Sort Series

• [1] 3가지의 기본 정렬: Selection, Bubble, Insertion Sort
• [2] 4가지의 고급 정렬: Quick, Merge, Heap, Tim Sort

---

지난 글에서 다룬 Selection Sort, Bubble Sort, Insertion Sort, 3가지의 기본 정렬 알고리즘은 이해하기 쉽고 구현이 간단하지만, 시간 복잡도가 최악의 경우 $O(n^2)$로, 큰 데이터셋에서는 성능이 크게 떨어진다는 한계가 있다.

이와 같은 이유로, 더 큰 데이터를 효율적으로 처리하기 위한 고급 정렬 알고리즘들이 등장했다.

이번 글에서는 Quick Sort, Merge Sort, Heap Sort, Tim Sort, 4가지 정렬 알고리즘을 통해 성능이 개선된 정렬 방식들을 알아보자.

---

1. Quick Sort (퀵 정렬)

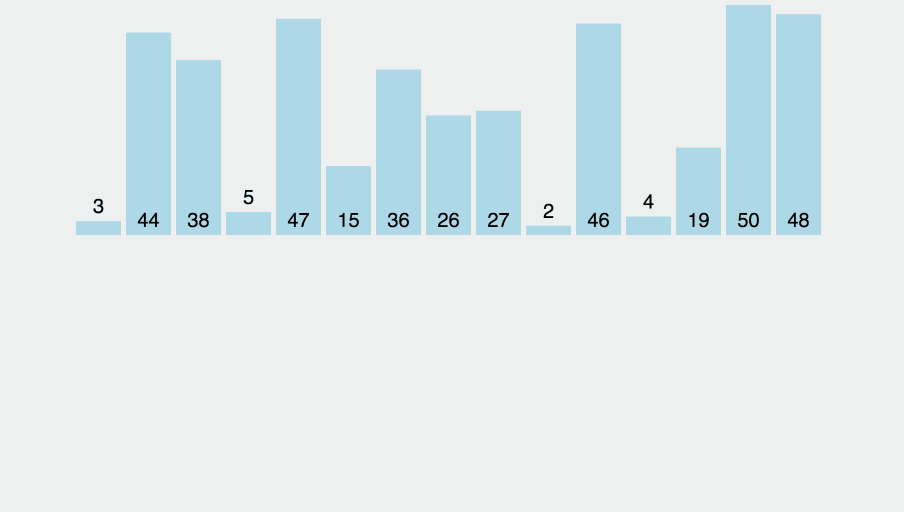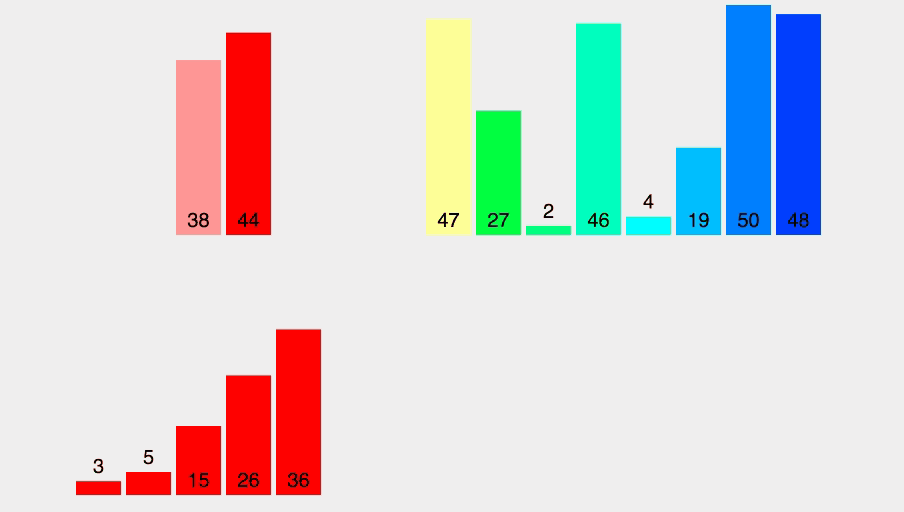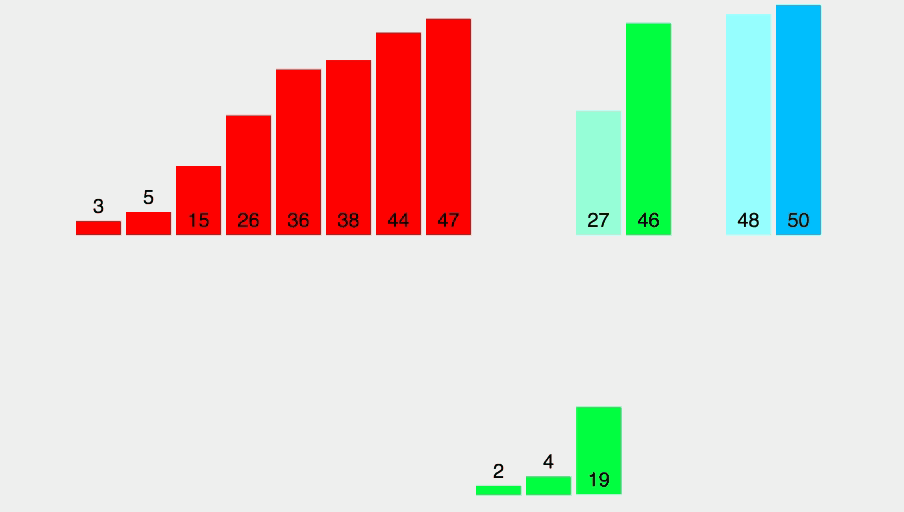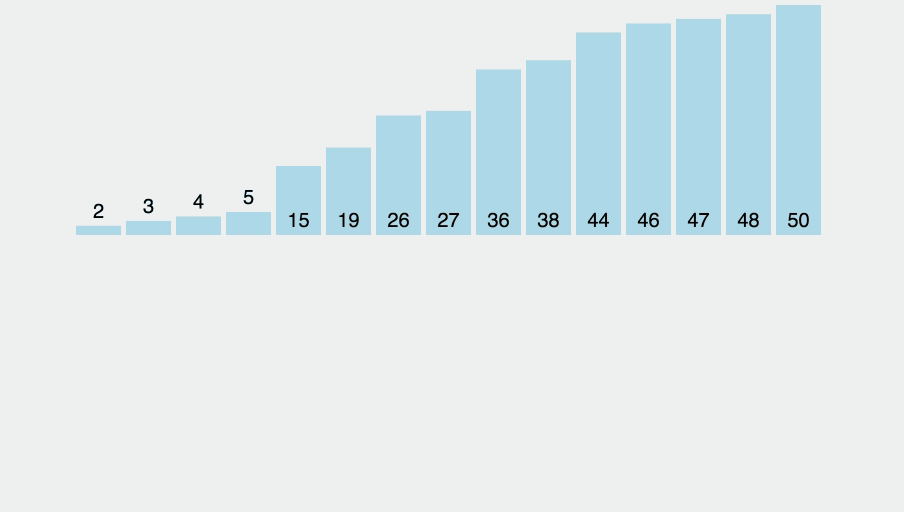
퀵 정렬은 분할 정복 전략을 활용해 데이터를 정렬한다.

리스트를 임의의 기준점으로 둘로 나눈 뒤, 기준보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 정렬한다.

이 과정을 재귀적으로 반복하여 전체 리스트를 정렬한다.

Quick Sort

퀵 정렬은 재귀적으로 리스트를 나누는 과정에서 평균적으로 $O(\log n)$ 단계로 분할되며, 각 단계마다 최대 n개의 연산이 필요하다.

시간 복잡도

평균 $O(n \log n)$, 최악의 경우 $O(n^2)$ (피벗이 한쪽에 치우친 경우)

퀵 정렬은 활용 방법에 따라 두 가지 구현 방법을 고려할 수 있다.

1. Stable but not In-place

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

위 코드는 가장 직관적인 퀵 정렬을 나타내며, 같은 값 순서가 유지되는 Stable 알고리즘이다.

Stable	분할 과정에서 left, middle, right 리스트에 추가될 때 순서가 유지된다.
Not In-place	새로운 리스트를 생성하므로, 별도 메모리 공간이 필요하다.

2. In-place but not Stable

def quick_sort_in_place(arr, low, high):
    if low >= high:
        return
    
    # 첫 번째 요소를 피벗으로 설정
    pivot = arr[low]
    left, right = low + 1, high

    while True:
        # 왼쪽 포인터가 피벗보다 큰 요소를 찾을 때까지 이동
        while left <= right and arr[left] <= pivot:
            left += 1
        # 오른쪽 포인터가 피벗보다 작은 요소를 찾을 때까지 이동
        while left <= right and arr[right] >= pivot:
            right -= 1
        
        if left > right:
            break
        else:
            # left와 right가 교차하지 않은 경우 요소 교환
            arr[left], arr[right] = arr[right], arr[left]
    
    # 피벗을 right 위치로 이동하여 분할 완료
    arr[low], arr[right] = arr[right], arr[low]

    # 재귀적으로 좌우 부분 리스트를 정렬
    quick_sort_in_place(arr, low, right - 1)
    quick_sort_in_place(arr, right + 1, high)

# Example usage
arr = [10, 7, 8, 9, 1, 5]
quick_sort_in_place(arr, 0, len(arr) - 1)

Not Stable	분할 과정에서 데이터 위치를 교환하기 때문에, 같은 값을 가진 데이터 순서가 유지되지 않는다.
In-place	배열 내에서 직접 정렬을 수행하며, 추가 메모리가 필요하지 않다.

---

2. Merge Sort (병합 정렬)

병합 정렬 역시 분할 정복 알고리즘을 활용하며, 리스트를 반으로 나눈 뒤, 각각의 리스트를 재귀적으로 정렬하고 2개의 정렬된 리스트를 병합하는 방식이다.

Merge Sort

병합 정렬은 리스트를 반으로 나눠 재귀적으로 정렬하고, 최종적으로 n개의 원소를 합병하는 과정을 반복한다.

Stable	병합 과정에서 원래 데이터의 순서를 유지하며 병합하므로, 같은 값을 가진 데이터 순서는 유지된다.
Not In-place	병합 과정에서 추가 배열이 필요하므로, 추가 메모리 공간이 요구된다.

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    
    result = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])
    result.extend(right[j:])
    return result

---

3. Heap Sort (힙 정렬)

힙 정렬은 힙(Heap) 자료 구조를 이용하여 정렬하는 알고리즘이다.

Heap: 완전 이진 트리 + 값 크기 조건 만족

완전 이진 트리	왼쪽에서 오른쪽 순서로 빈틈 없이 채워진 이진 트리
값 크기 조건 만족	부모 노드와 자식 노드 간의 크기 관계에 따라 최대 힙, 최소 힙으로 정의될 수 있음

주로 최대 힙을 사용하며, 리스트의 최댓값을 추출해 정렬을 수행한다. 이 과정에서 힙을 재구성해 정렬이 완료될 때까지 반복한다.

Heap Sort

시간 복잡도	모든 경우 $O(n \log n)$
Not Stable	힙을 재구성하면서 데이터의 순서를 고려하지 않는다.
In-place	힙을 배열 내에서 정렬하므로 추가 메모리는 필요하지 않다.

def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2
    
    if left < n and arr[left] > arr[largest]:
        largest = left
    if right < n and arr[right] > arr[largest]:
        largest = right
    
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)
    
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
    
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)
    return arr

---

4. Tim Sort (팀 정렬)

팀 정렬은 파이썬의 내장 정렬 함수인 sorted()와 sort()에서 사용되는 알고리즘이다.

병합 정렬과 삽입 정렬을 결합해 만든 하이브리드 정렬 알고리즘이다.

일정 길이 이하의 작은 리스트에는 삽입 정렬을 사용하고, 그 이상에는 병합 정렬을 사용한다.

# 팀 정렬은 파이썬 내장 함수로 이미 구현됨
arr = [4, 2, 7, 1, 9, 3]
sorted_arr = sorted(arr)
print(sorted_arr)

정리

4가지 고급 정렬 알고리즘의 성능을 정리하면 다음과 같다.

구분	Quick Sort(In-place)	Merge Sort	Heap Sort	Tim Sort
Worst Case	$O(n^2)$	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$
Avg Case	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$
Best Case	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$
Stable	No	Yes	No	Yes
In-place	Yes	No	Yes	No

---

Reference

1. 신찬수 교수 유튜브
2. 파이썬 알고리즘 인터뷰